Programming Interview Questions 21: Tree Reverse Level Order Print

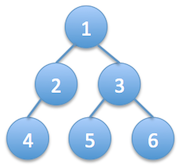
This is very similar to the previous post level order print. We again print the tree in level order, but now starting from bottom level to the root. Using the same tree as before:

The output should be:
4 5 6
2 3
1

The solution of this problem is similar to level order print. We start a breadth first search (BFS) from the root of the tree and push each node to a queue. We don’t print any node at this point because we want to output bottom up, but BFS progresses from top to bottom. Printing will be take place a separate loop after completing breadth first search. We also count the number of nodes in each level and push them to a stack, in order to print the new lines in correct places. So after completion of BFS we have the following two data structures:

Queue of nodes: [1, 2, 3, 4, 5, 6]. This queue is constructed by BFS from top to bottom and left to right.
Stack of node counts at each level: [3, 2, 1]. Note that since this is a stack the first element is the node count at the deepest level, and the last count is always 1 which corresponds to the root of the tree.

After constructing these data structures, the nodes we want to print as the first line of output are at the end of the queue. And the number of nodes to print is at the top of the stack. So we start a loop where at each iteration we pop an element from the stack and print that many number of nodes from the end of the queue. Using the example tree above, the first line of the output contains 3 nodes, the first element in the stack. And the nodes to print are the 3 nodes at the end of the queue, which is [4, 5, 6]. The second line of the output contains 2 nodes, the second value in the stack. These are the 2 nodes in the queue that are just before the first line nodes, namely [2, 3]. Finally, the number of nodes in the last line is at the end of the stack, which is 1. And the node to print is at the beginning of the queue, the value 1.

Here is the code:

class Node:
    def __init__(self, val=None):
        self.left, self.right, self.val = None, None, val
    def __repr__(self):
        return str(self.val)
 
def reverseLevelOrderPrint(tree):
    if not tree:
        return
    nodes=[tree]    #queue
    levelCount=collections.deque([1])   #stack
    currentCount, nextCount = 1, 0
    i=0
    while i<len(nodes):
        currentNode=nodes[i]
        currentCount-=1
        if currentNode.left:
            nodes.append(currentNode.left)
            nextCount+=1
        if currentNode.right:
            nodes.append(currentNode.right)
            nextCount+=1
        if nextCount==0:
            #no more nodes at next level
            break
        if currentCount==0:
            #finished this level
            levelCount.appendleft(nextCount)
            currentCount, nextCount = nextCount, currentCount
        i+=1
    printIndex=len(nodes)
    for count in levelCount:
        output=nodes[printIndex-count:printIndex]
        print ' '.join(map(str, output)), '\n',
        printIndex-=count

This is a great question that uses the most fundamental data structures: tree, stack, and queue.