Programming Interview Questions 23: Find Word Positions in Text

Given a text file and a word, find the positions that the word occurs in the file. We’ll be asked to find the positions of many words in the same file.

Since we’ll have to answer multiple queries, precomputation would be useful. We’ll build a data structure that stores the positions of all the words in the text file. This is known as inverted index in Information Retrieval. It’s basically a mapping between the words in the file and their positions. You can read more about it in my how to implement a search engine post, where I describe how to actually implement a working search engine with real code.

We can use hashtable as our inverted index. The key is a word in the file, and the value is the array of positions that word occurs. So, we’ll get all the words in the file and populate the hashtable with their positions. The words may contain capital letters, but we don’t want separate entries for apple, and Apple in our inverted index. So, we’ll write our  own parsing function which converts all the words to lowercase, eliminates non-alphanumeric characters, and then splits on whitespace to get all the actual words in the file. We can do it easily using regular expressions:

def getWords(text):
    return re.sub(r'[^a-z0-9]',' ',text.lower()).split()

The function first converts all letters to lowercase, then replaces non-alphanumeric characters with space, and splits on whitespace. The result is all the words in their original order. Then we build the inverted index by looping over the words in the file we just got, and append the position of each word to its list of positions in the hashtable:

def createIndex1(text):
    index=collections.defaultdict(list)
    words=getWords(text)
    for pos, word in enumerate(words):
        index[word].append(pos)
    return index

Once we build the index we can answer any query. Given a word, just return its position array if it exists in the hashtable index. Otherwise, if the word isn’t present in the index, it means that the word doesn’t appear in the file, so return an empty list. Here’s the code:

def queryIndex1(index, word):
    if word in index:
        return index[word]
    else:
        return []

This is it actually! We have built a search engine for a single file, if we generalize it to work on multiple files (web pages) we’ll have a basic search engine. The complexity of create index is O(N), linear in the number of words in the text. The complexity of query index is constant O(1), because it’s just a simple lookup operation in the hashtable index. So, both creating the index and querying for word positions is optimal. The space complexity is also O(N), linear in the number of words. Because we have each word as a key in the hashtable.

Better Solution
Using hashtable as the inverted index is pretty efficient. But we can do better by using a more space efficient data structure for text, namely a , also known as prefix tree. Trie is a tree which is very efficient in text storage and search. It saves space by letting the words that have the same prefixes to share data. And most languages contain many words that share the same prefix.

Let’s demonstrate this with an example using the words subtree, subset, and submit. In a hashtable index, each of these words will be stored separately as individual keys. So, it will take 7+6+6=19 characters of space in the index. But all these words share the same prefix ‘sub’. We can take advantage of this fact by using a trie and letting them share that prefix in the index. In a trie index these words will take 7+3+3=13 characters of space, cutting the size of the index around 30%. We can have even more gain with the words that share longer prefixes. For example author, authority, and authorize. Hashtable index uses 6+9+9=24 characters but trie uses only 6+3+2=11, leading to 55% compression. Considering the extremely big web indexes of search engines, reducing the index size even by 10% is a big gain, which results in saving terabytes of space and reduces the number of machines by 1/10. Which is huge given that thousands of machines are used at Google, Microsoft, and Yahoo.

To summarize, it’s very useful to use a trie while performing storage and retrieval on text data. There are existing implementations of tries, but they’re more complicated than we actually need. So let’s implement our own simple trie, it’ll be more fun and informative.

A trie is simply a tree where each node stores a character as key, and the value in our case will be the occurrence positions of the word associated with the node. The word associated with a node is concatenation of the characters from root of the tree to the node. Every node in the tree has a corresponding word, but not all of them are valid English words. Most of them are intermediate words. Only the words that occur in the given text will contain position data. We call these nodes terminal nodes. Maximum number of children of a node is the number of different characters that appear in the text, which is 36 if we only consider lowercase alphanumeric characters. Here is the structure of a node:

class Node:
    def __init__(self, letter):
        self.letter=letter
        self.isTerminal=False
        self.children={}
        self.positions=[]

The trie data structure is composed of these nodes, and it’ll include the following 3 functions: getItem, contains, and output. The getItem function both returns the occurrence positions of a given word and it’s used for insertion, contains function checks whether a word is in the trie or not, and output prints the trie in a nice formatted manner. We insert a new occurrence position to a word by first getting its existing position list using the getItem function, and then appending the new position to the end of the list. Trying to access an element that’s not in the trie automatically creates that element, similar to . Code of getItem and contains functions are very similar. Both navigate through the tree until they reach the node that corresponds to the given word. Output prints the words in the trie in sorted order and indented in a way that prefix relations can be visually identified. Here’s the complete implementation:

class Trie:
    def __init__(self):
        self.root=Node('')        
 
    def __contains__(self, word):
        current=self.root
        for letter in word:
            if letter not in current.children:
                return False
            current=current.children[letter]
        return current.isTerminal
 
    def __getitem__(self, word):
        current=self.root
        for letter in word:
            if letter not in current.children:
                current.children[letter]=Node(letter)
            current=current.children[letter]
        current.isTerminal=True
        return current.positions
 
    def __str__(self):
        self.output([self.root])
        return ''
 
    def output(self, currentPath, indent=''):
        #Depth First Search
        currentNode=currentPath[-1]
        if currentNode.isTerminal:
            word=''.join([node.letter for node in currentPath])
            print indent+word+' '+str(currentNode.positions)
            indent+='  '
        for letter, node in sorted(currentNode.children.items()):
            self.output(currentPath[:]+[node], indent)

New createIndex and queryIndex functions are very similar to hashtable ones:

def createIndex2(text):
    trie=Trie()
    words=getWords(text)
    for pos, word in enumerate(words):
        trie[word].append(pos)
    return trie
 
def queryIndex2(index, word):
    if word in index:
        return index[word]
    else:
        return []

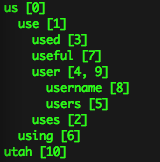
Let’s see an example trie constructed from words that share prefixes, here’s an artificial example text for demo: ‘us use uses used user users using useful username user utah’. The output function prints the following trie:

Indentation is based on shared word prefixes. For example used, useful, and user all share the prefix word use, so they’re indented. Also username and users share the prefix word user. But us and utah are at the same indentation level because the prefix they share (character u) is not a proper word. The values of words are their occurrence positions in the text.

The complexity of adding or finding an element in a trie is also constant O(1), like hashtable. It doesn’t depend on the number of words stored in the trie, it only depends on the number of characters in the word, just like hashing. And maximum number of characters in a word for a particular language is constant. Average number of characters in an English word is around 4-5, and most of them are shorter than 15. Which means it’ll generally take around 4-5 operations, and mostly less than 15, to find a word in the trie independent of the number of words stored. It can be millions or even billions, the complexity stays the same. Which is perfect, because it’s not linear on the number of words, instead it’s just a constant number.

This is personally one of my favorite questions because we actually implement a basic search engine that operates on a single file, and can easily be extended to search multiple files. If you would like to see how to build an actual search engine with working code, I recommend my previous posts: create index, query index, and ranking.