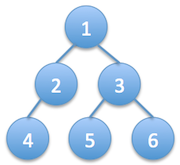
The output should be:
1
2 3
4 5 6

It won’t be practical to solve this problem using recursion, because recursion is similar to depth first search, but what we need here is breadth first search. So we will use a queue as we did previously in breadth first search. First, we’ll push the root node into the queue. Then we start a while loop with the condition queue not being empty. Then, at each iteration we pop a node from the beginning of the queue and push its children to the end of the queue. Once we pop a node we print its value and space.

To print the new line in correct place we should count the number of nodes at each level. We will have 2 counts, namely current level count and next level count. Current level count indicates how many nodes should be printed at this level before printing a new line. We decrement it every time we pop an element from the queue and print it. Once the current level count reaches zero we print a new line. Next level count contains the number of nodes in the next level, which will become the current level count after printing a new line. We count the number of nodes in the next level by counting the number of children of the nodes in the current level. Understanding the code is easier than its explanation:

class Node:
    def __init__(self, val=None):
        self.left, self.right, self.val = None, None, val        
 
def levelOrderPrint(tree):
    if not tree:
        return
    nodes=collections.deque([tree])
    currentCount, nextCount = 1, 0
    while len(nodes)!=0:
        currentNode=nodes.popleft()
        currentCount-=1
        print currentNode.val,
        if currentNode.left:
            nodes.append(currentNode.left)
            nextCount+=1
        if currentNode.right:
            nodes.append(currentNode.right)
            nextCount+=1
        if currentCount==0:
            #finished printing current level
            print '\n',
            currentCount, nextCount = nextCount, currentCount

The time complexity of this solution is O(N), which is the number of nodes in the tree, so it’s optimal. Because we should visit each node at least once. The space complexity depends on maximum size of the queue at any point, which is the most number of nodes at one level. The worst case occurs when the tree is a complete binary tree, which means each level is completely filled with maximum number of nodes possible. In this case, the most number of nodes appear at the last level, which is (N+1)/2 where N is the total number of nodes. So the space complexity is also O(N). Which is also optimal while using a queue.

This is one of the most common tree interview questions and everyone should know it off the top of their head.

The naive algorithm is to increment the number until we get a palindrome. So at every iteration we check whether the new number is palindrome or not. This is the most straightforward non-optimal solution. The complexity depends on the number of digits in the number. If the number has 6 digits, we may have to increment it 999 times to get the smallest palindrome in the worst case (999000 to 999999). So the complexity is O(sqrt(N)), which is pretty bad. We can do it in constant O(1) time by using clever tricks.

There are two cases, whether the number of digits in the number is odd or even. We’ll start with analyzing the odd case. Let’s say the number is ABCDE, the smallest possible palindrome we can obtain from this number is ABCBA, which is formed by mirroring the number around its center from left to right (copying the left half onto the right in reverse order). This number is always a palindrome, but it may not be greater than the original number. If it is then we simply return the number, if not we increase the number. But which digit to increment? We don’t want to increment the digits on the left half because they increase the number substantially, and we’re looking for the smallest palindrome larger than the number. The digits on the right half increase the value of the number much less, but then to keep the number palindrome we’ll have to increment the digits on the left half as well, which will again result in a large increase. So, we increment the digit just in the middle by 1, which corresponds to adding 100 in this case. This way the number stays a palindrome, and the resulting number is always larger than the original number.

Here are some examples to clarify any doubt. Let’s say the given number is 250, we first take the mirror image around its center, resulting in 252. 252 is greater than 250 so this is the first palindrome greater than the given number, we’re done. Now let’s say the number is 123, now mirroring the number results in 121, which is less than the original number. So we increment it’s middle digit, resulting in 131. This is again the first smallest palindrome larger than the number. But what if the middle digit is 9 and mirroring the number results in a smaller value? Then simply incrementing the middle digit would not work. The solution is we first round up the number and then apply the procedure to it. For example if the number is 397, mirroring results in 393 which is less. So we round it up to 400 and solve the problem as if we got 400 in the first place. We take the mirror image, which is 404 and this is the result.

Now let’s analyze the case where the given number has even number of digits. Let’s say the given number is ABCD, similar to the odd case the smallest possible palindrome we can obtain from this number is ABBA (and yes their songs are awesome :). Again we did the mirror image around its center from left to right. But since the number has even number of digits the center now lies between 2nd (C, tenth digit) and 3rd (B, hundredth) digits (counting from right starting at 1). So let’s define the center digit as the middle two digits, 2nd and 3rd in our case. The strategy to find the next palindrome is same. First we mirror the number and check whether it’s greater than the given one. If it is then we return that number, if not we increment the middle two digits by 1, which means adding 110 in this case. Let’s again see some examples.

Assume the given number is 4512, we mirror the number around its center, resulting in 4554. This is greater than the given number so we’re done. Now let the number be 1234, mirroring results in 1221 which is less than the original number. So we increment the middle two digits, resulting in 1331 which is the result. What if the middle digits become 9 after mirroring and the resulting number is smaller than the original one? Then we again round up the number and solve the problem as if we got the round number in the first place. For example, if the given number is 1997 mirroring would give 1991, which is less. So we round it up to 2000 and solve as if it were the original number. We mirror it, resulting in 2002 and this is the result. The code will make everything clear:

def nextPalindrome(num):
    length=len(str(num))
    oddDigits=(length%2!=0)
    leftHalf=getLeftHalf(num)
    middle=getMiddle(num)
    if oddDigits:
        increment=pow(10, length/2)
        newNum=int(leftHalf+middle+leftHalf[::-1])
    else:
        increment=int(1.1*pow(10, length/2))
        newNum=int(leftHalf+leftHalf[::-1])
    if newNum>num:
        return newNum
    if middle!='9':
        return newNum+increment
    else:
        return nextPalindrome(roundUp(num))
 
def getLeftHalf(num):
    return str(num)[:len(str(num))/2]
 
def getMiddle(num):
    return str(num)[(len(str(num))-1)/2]
 
def roundUp(num):
    length=len(str(num))
    increment=pow(10,((length/2)+1))
    return ((num/increment)+1)*increment

The complexity of this algorithm is O(1), because we perform at most 3 operations per number, which is when the middle digit is 9 (2 mirroring and 1 incrementing). Otherwise we perform 2 operations operations at most (mirroring and incrementing). In the best case only 1 operation suffices, just mirroring.

I personally like this question because it involves some simple math and creative thinking.

We can use a hashtable as we always do with problems that involve counting. Scan the array and count the occurrences of each number. Then perform a second pass from the hashtable and return the element with even count. Here’s the code:

def getEven1(arr):
    counts=collections.defaultdict(int)
    for num in arr:
        counts[num]+=1
    for num, count in counts.items():
        if count%2==0:
            return num

Time and space complexity of this approach is O(N), which is optimal. There’s also another equally efficient but more elegant solution using the XOR trick I explained in my previous post find missing element. First we get all the unique numbers in the array using a set in O(N) time. Then we XOR the original array and the unique numbers all together. Result of XOR is the even occurring element. Because every odd occurring element in the array will be XORed with itself odd number of times, therefore producing a 0. And the only even occurring element will be XORed with itself even number of times, which is the number itself. The order of XOR is not important. The conclusion is that if we XOR a number with itself odd number of times we get 0, otherwise if we XOR even number of times then we get the number itself. And with multiple numbers, the order of XOR is not important, just how many times we XOR a number with itself is significant.

For example, let’s say we’re given the following array: [2, 1, 3, 1]. First we get all the unique elements [1, 2, 3]. Then we construct a new array from the original array and the unique elements by appending them together [2, 1, 3, 1, 1, 2, 3]. We XOR all the elements in this new array. The result is 2^1^3^1^1^2^3 = 1. Because the numbers 2 and 3 occur in the new array even number of times (2 times), so they’ll be XORed with themselves odd times (1 time), which results in 0. The number 1 occurs odd number of times (3 times), so it’ll be XORed with itself even times (2 times), and the result is the number 1 itself. Which is the even occurring element in the original array. Here’s the code of this approach:

def getEven2(arr):
    return reduce(lambda x, y: x^y, arr+list(set(arr)))

Time and complexity of this approach is also O(N). Note that I assume O(1) insert and find in both hashtable and set, which is mostly the case in the average. But the actual worst case complexity depends on the implementation and the programming language used. It can be logarithmic, or even linear. But in an interview setting I think it’s safe to assume constant time insert and find in both hashtable and set.

The straightforward solution is to scan the array linearly until we find the number, or go out of bounds and get an exception. In the former case we return the index, the latter case returns -1. The complexity is O(N) where N is the number of elements in the array that we don’t know in advance. However, in this approach we are not taking advantage of the array being sorted. So we can use some sort of binary search to benefit from sorted order.

Standard binary search wouldn’t work because we don’t know the size of the array to provide an upper limit index. So, we perform one-sided binary search for both the size of the array and the element itself simultaneously. Let’s say we’re searching for the value k. We check array indexes 0, 1, 2, 4, 8, 16, …, 2^N in a loop until either we get an exception or we see an element larger than k. If the value is less than k we continue, or if we luckily find the actual value k then we return the index.

If at index 2^m we see an element larger than k, it means the value k (if it exists) must be between indexes 2^(m-1)+1 and 2^m-1 (inclusive), since the array is sorted. The same is true if we get an exception, because we know that the number at index 2^(m-1) is less than k, and we didn’t get an exception accessing that index. Getting an exception at index 2^m means the size of the array is somewhere between 2^(m-1) and 2^m-1. In both cases we break out of the loop and start another modified binary search, this time between indexes 2^(m-1)+1 and 2^m-1. If we previously got exception at index 2^m, we may get more exceptions during this binary search so we should handle this case by assigning the new high index to that location. The code will clarify everything:

def getIndex(arr, num):
    #check array indexes 0, 2^0, 2^1, 2^2, ...
    index, exp = 0, 0
    while True:
        try:
            if arr[index]==num:
                return index
            elif arr[index]<num:
                index=2**exp
                exp+=1
            else:
                break
        except IndexError:
            break
 
    #Binary Search
    left=(index/2)+1
    right=index-1
    while left<=right:
        try:
            mid=left+(right-left)/2
            if arr[mid]==num:
                return mid
            elif arr[mid]<num:
                left=mid+1
            else:
                right=mid-1
        except IndexError:
            right=mid-1
 
    return -1

The complexity of this approach is O(logN) because we use binary search all the time, we never perform a linear scan. So it’s optimal. Binary search is one of the most important algorithms and this question demonstrates an interesting use of it.

First we should extract only the letters from both strings and convert to lowercase, excluding punctuation and whitespaces. Then we can compare these to check whether two strings are anagrams of each other. From now on when I refer to a string, I assume this transformation is performed and it only contains lowercase letters in original order.

If two strings contain every letter same number of times, then they are anagrams. One way to perform this check is to sort both strings and check whether they’re the same or not. The complexity is O(NlogN) where N is the number of characters in the string. Here’s the code:

def isAnagram1(str1, str2):
    return sorted(getLetters(str1))==sorted(getLetters(str2))
 
def getLetters(text):
    return [char.lower() for char in text if char in string.letters]

Sorting approach is elegant but not optimal. We would prefer a linear time solution. Since the problem involves counting, hashtable would be a suitable data structure. We can store the counts of each character in string1 in a hashtable. Then we scan string2 from left to right decreasing the count of each letter. Once the count becomes negative (string2 contains more of that character) or if the letter doesn’t exist in the hashtable (string1 doesn’t contain that character), then the strings are not anagrams. Finally we check whether all the counts in the hashtable are 0, otherwise string1 contains extra characters. Or we can check the lengths of the strings in the beginning and avoid this count check. This also allows early termination of the program if the strings are of different lengths, because they can’t be anagrams. The code is the following:

def isAnagram2(str1, str2):
    str1, str2 = getLetters(str1), getLetters(str2)
    if len(str1)!=len(str2):
        return False
    counts=collections.defaultdict(int)
    for letter in str1:
        counts[letter]+=1
    for letter in str2:
        counts[letter]-=1
        if counts[letter]<0:
            return False
    return True

I use python’s defaultdict as hashtable. If a letter doesn’t exist in the dictionary it produces the value of 0. The complexity of this solution is O(N), which is optimal. The use of hashtables in storing counts once again proves its advantage.

This question demonstrates efficient use of hashtable. We scan the string from left to right counting the number occurrences of each character in a hashtable. Then we perform a second pass and check the counts of every character. Whenever we hit a count of 1 we return that character, that’s the first unique letter. If we can’t find any unique characters, then we don’t return anything (None in python). Here’s the code:

def firstUnique(text):
    counts=collections.defaultdict(int)
    for letter in text:
        counts[letter]+=1
    for letter in text:
        if counts[letter]==1:
            return letter

As you can see it’s pretty straightforward once we use a hashtable. It’s an optimal solution, the complexity is O(N). Hashtable is generally the key data structure to achieve optimal linear time solutions in questions that involve counting.

This is another data structure question, if we use the correct one it’s pretty straightforward. We scan the string from left to right, and every time we see an opening parenthesis we push it to a stack, because we want the last opening parenthesis to be closed first. Then, when we see a closing parenthesis we check whether the last opened one is the corresponding closing match, by popping an element from the stack. If it’s a valid match, then we proceed forward, if not return false. Or if the stack is empty we also return false, because there’s no opening parenthesis associated with this closing one. In the end, we also check whether the stack is empty. If so, we return true, otherwise return false because there were some opened parenthesis that were not closed. Here’s the code:

def isBalanced(expr):
    if len(expr)%2!=0:
        return False
    opening=set('([{')
    match=set([ ('(',')'), ('[',']'), ('{','}') ])
    stack=[]
    for char in expr:
        if char in opening:
            stack.append(char)
        else:
            if len(stack)==0:
                return False
            lastOpen=stack.pop()
            if (lastOpen, char) not in match:
                return False
    return len(stack)==0

This is a simple yet common interview question that demonstrates correct use of a stack.

This is a data structure question. We will insert the received numbers into such a data structure that we’ll be able to find the median very efficiently. Let’s analyse the possible options.

We can insert the integers to an unsorted array, so we’ll just append the numbers to the array one by one as we receive. Insertion complexity is O(1) but finding the median will take O(N) time, if we use the Median of Medians algorithm that I described in my previous post. However, our goal is to find the median most efficiently, we don’t care that much about insertion performance. But this algorithm does the exact opposite, so unsorted array is not a feasible solution.

What about using a sorted array? We can find the position to insert the received number in O(logN) time using binary search. And at any time if we’re asked for the median we can just return the middle element if the array length is odd, or the average of middle elements if the length is even. This can be done in O(1) time, which is exactly what we’re looking for. But there’s a major drawback of using a sorted array. To keep the array sorted after inserting an element, we may need to shift the elements to the right, which will take O(N) time. So, even if finding the position to insert the number takes O(logN) time, the overall insertion complexity is O(N) due to shifting. But finding the median is still extremely efficient, constant time. However, linear time insertion is pretty inefficient and we would prefer a better performance.

Let’s try linked lists. First unsorted linked list. Insertion is O(1), we can insert either to the head or tail but we suffer from the same problem of unsorted array. Finding the median is O(N). What if we keep the linked list sorted? We can find the median in O(1) time if we keep track of the middle elements. Insertion to a particular location is also O(1) in any linked list, so it seems great thus far. But, finding the right location to insert is not O(logN) as in sorted array, it’s instead O(N) because we can’t perform binary search in a linked list even if it is sorted. So, using a sorted linked list doesn’t worth the effort, insertion is O(N) and finding median is O(1), same as the sorted array. In sorted array insertion is linear due to shifting, here it’s linear because we can’t do binary search in a linked list. This is a very fundamental data structure knowledge that we should keep at the top of our heads all the time.

Using a stack or queue wouldn’t help as well. Insertion would be O(1) but finding the median would be O(N), very inefficient.

What if we use trees? Let’s use a binary search tree with additional information at each node, number of children on the left and right subtrees. We also keep the number of total nodes in the tree. Using this additional information we can find the median in O(logN) time, taking the appropriate branch in the tree based on number of children on the left and right of the current node. However, the insertion complexity is O(N) because a standard binary search tree can degenerate into a linked list if we happen to receive the numbers in sorted order.

So, let’s use a balanced binary search tree to avoid worst case behaviour of standard binary search trees. In a height balanced binary search tree (i.e. AVL tree) the balance factor is the difference between the heights of left and right subtrees. A node with balance factor 0, +1, or -1 is considered to be balanced. However, in our tree the balance factor won’t be height, it is the number of nodes in the left subtree minus the number of nodes in the right subtree. And only the nodes with balance factor of +1 or 0 are considered to be balanced. So, the number of nodes on the left subtree is either equal to or 1 more than the number of nodes on the right subtree, but not less. If we ensure this balance factor on every node in the tree, then the root of the tree is the median, if the number of elements is odd. In the even case, the median is the average of the root and its inorder successor, which is the leftmost descendent of its right subtree. So, complexity of insertion maintaining balance condition is O(logN) and find median operation is O(1) assuming we calculate the inorder successor of the root at every insertion if the number of nodes is even. Insertion and balancing is very similar to AVL trees. Instead of updating the heights, we update the number of nodes information.

Balanced binary search trees seem to be the most optimal solution, insertion is O(logN) and find median is O(1). Can we do better? We can achieve the same complexity with a simpler and more elegant solution. We will use 2 heaps simultaneously, a max-heap and a min-heap with 2 requirements. The first requirement is that the max-heap contains the smallest half of the numbers and min-heap contains the largest half. So, the numbers in max-heap are always less than or equal to the numbers in min-heap. Let’s call this the order requirement. The second requirement is that, the number of elements in max-heap is either equal to or 1 more than the number of elements in the min-heap. So, if we received 2N elements (even) up to now, max-heap and min-heap will both contain N elements. Otherwise, if we have received 2N+1 elements (odd), max-heap will contain N+1 and min-heap N. Let’s call this the size requirement.

The heaps are constructed considering the two requirements above. Then once we’re asked for the median, if the total number of received elements is odd, the median is the root of the max-heap. If it’s even, then the median is the average of the roots of the max-heap and min-heap. Let’s now analyse why this approach works, and how we construct the heaps.

We will have two methods, insert a new received number to the heaps and find median. The insertion procedure takes the two requirements into account, and it’s executed every time we receive a new element. We take two different approaches depending on whether the total number of elements is even or odd before insertion.

Let’s first analyze the size requirement during insertion. In both cases we insert the new element to the max-heap, but perform different actions afterwards. In the first case, if the total number of elements in the heaps is even before insertion, then there are N elements both in max-heap and min-heap because of the size requirement. After inserting the new element to the max-heap, it contains N+1 elements but this doesn’t violate the size requirement. Max-heap can contain 1 more element than min-heap. In the second case, if the number of elements is odd before insertion, then there are N+1 elements in max-heap and N in min-heap. After we insert the new element to the max-heap, it contains N+2 elements. But this violates the size constraint, max-heap can contain at most 1 more element than min-heap. So we pop an element from max-heap and push it to min-heap. The details will be described soon.

Now let’s analyse the order requirement. This requirement forces every element in the max-heap to be less than or equal to all the elements in min-heap. So the max-heap contains the smaller half of the numbers and the min-heap contains the larger half. Note that by design the root of the max-heap is the maximum of the lower half, and root of the min-heap is the minimum of the upper half. Keeping these in mind, we again take two different actions depending on whether the total number of elements is even or odd before insertion. In the even case we just inserted the new element to the max-heap. If the new element is less than all the elements in the min-heap, then the order constraint is satisfied and we’re done. We can perform this check by comparing the new element to the root of the min-heap in O(1) time since the root of the min-heap is the minimum. But if the new element is larger than the root of min-heap then we should exchange those elements to satisfy the order requirement. Note that in this case the root of the max-heap is the new element. So we pop the the root of min-heap and insert it to max-heap. Also pop the root of max-heap and insert it to min-heap. In second case, where the total number of elements before insertion is odd, we inserted the new element to max-heap, then we popped an element and pushed it to the min-heap. To satisfy the order constraint, we pop the maximum element of the max-heap, the root, and insert it to the min-heap. Insertion complexity is O(logN), which is the insertion complexity of a heap.

That is exactly how the insertion procedure works. We ensured that both size and order requirements are satisfied during insertion. Find median function works as follows. At any time we will be queried for the median element. If the total number of elements at that time is odd, then the median is the root of the max-heap. Let’s visualize this with an example. Assume that we have received 7 elements up to now, so the median is the 4th number in sorted order. Currently, max-heap contains 4 smallest elements and min-heap contains 3 largest because of the requirements described above. And since the root of the max-heap is the maximum of the smallest four elements, it’s the 4th element in sorted order, which is the median. Else if the total number of elements is odd, then the median is the average of the roots of max-heap and min-heap. Let’s say we have 8 elements, so the median is the average of 4th and 5th elements in sorted order. Currently, both the max-heap and min-heap contain 4 numbers. Root of the max-heap is the maximum of the smallest numbers, which is 4th in sorted order. And root of the min-heap is the minimum of the largest numbers, which is 5th in sorted order. So, the median is the average of the roots. In both cases we can find the median in O(1) time because we only access the roots of the heaps, neither insertion nor removal is performed. Therefore, overall this solution provides O(1) find heap and O(logN) insert.

A code is worth a thousand words, here is the code of the 2-heaps solution. As you can see, it’s much less complicated than it’s described. We can use the heapq module in python, which provides an implementation of min-heap only. But we need a max-heap as well, so we can make a min-heap behave like a max-heap by multiplying the number to be inserted by -1 and then inserting. So, every time we insert or access an element from the max-heap, we multiply the value by -1 to get the original number:

class streamMedian:
    def __init__(self):
        self.minHeap, self.maxHeap = [], []
        self.N=0
 
    def insert(self, num):
        if self.N%2==0:
            heapq.heappush(self.maxHeap, -1*num)
            self.N+=1
            if len(self.minHeap)==0:
                return
            if -1*self.maxHeap[0]>self.minHeap[0]:
                toMin=-1*heapq.heappop(self.maxHeap)
                toMax=heapq.heappop(self.minHeap)
                heapq.heappush(self.maxHeap, -1*toMax)
                heapq.heappush(self.minHeap, toMin)
        else:
            toMin=-1*heapq.heappushpop(self.maxHeap, -1*num)
            heapq.heappush(self.minHeap, toMin)
            self.N+=1
 
    def getMedian(self):
        if self.N%2==0:
            return (-1*self.maxHeap[0]+self.minHeap[0])/2.0
        else:
            return -1*self.maxHeap[0]

We have a class streamMedian, and every time we receive an element, insert function is called. The median is returned using the getMedian function.

This is a great interview question that tests data structure fundamentals in a subtle way.

This can be done pretty easily in python since it has very useful functions to do most of the work itself. Split on whitespace (removes multiple contiguous spaces as well as leading and trailing spaces) and reverse the order of words. There are two alternative one-liners:

def reverseWords1(text):
    print " ".join(reversed(text.split()))
 
def reverseWords2(text):
    print " ".join(text.split()[::-1])

But this kind of seems like cheating since python is doing most of the heavy work for us. Let’s do more work by looping over the text and extracting the words ourselves instead of using the function split. We push the words to a stack and in the end pop all to reverse. Here is the code:

def reverseWords3(text):
    words=[]
    length=len(text)
    space=set(string.whitespace)
    index=0
    while index<length:
        if text[index] not in space:
            wordStart=index
            while index<length and text[index] not in space:
                index+=1
            words.append(text[wordStart:index])
        index+=1
 
    print " ".join(reversed(words))

All these solutions use extra space (stack or constructing a new list), but we can in fact solve it in-place. Reverse all the characters in the string, then reverse the letters of each individual word. This can be done in-place using C or C++. But since python strings are immutable we can’t modify them in-place, any modification to a string returns a new string. Here’s the python code which uses the same logic but not in-place:

def reverseWords4(text):
    words=text[::-1].split()
    print " ".join([word[::-1] for word in words])

In C/C++ we would first reverse the entire string and loop over it with two pointers, read and write. We’ll overwrite the string in-place. The resulting string may be shorter than the original one, because we have to remove multiple consecutive spaces as well as leading and trailing ones, that’s why we need 2 pointers. But note that write pointer can never pass read pointer so there won’t be any conflicts. Here is the C code:

void reverseWords(char *text)
{
    int length=strlen(text);
    reverseString(text, 0, length-1, 0);
    int read=0, write=0;
    while (read<length)
    {
        if (text[read]!=' ')
        {
            int wordStart=read;
            for ( ;read<length && text[read]!=' '; read++);
            reverseString(text, wordStart, read-1, write);
            write+=read-wordStart;
            text[write++]=' ';
        }
        read++;
    }
    text[write-1]='\0';
}
 
void reverseString(char *text, int start, int end, int destination)
{
    // reverse the string and copy it to destination
    int length=end-start+1;
    int i;
    memcpy(&text[destination], &text[start], length*sizeof(char));
    for (i=0; i<length/2; i++)
    {
        swap(&text[destination+i], &text[destination+length-1-i]);
    } 
}

This is one of the most common interview questions, so anyone preparing for interviews should be able to solve it hands down.

This may seem hard at first but it’s in fact pretty easy once we figure out the logic. Let’s say we’re given a string of length N, and we somehow generated some permutations of length N-1. How do we generate all permutations of length N? Demonstrating with a small example will help. Let the string be ‘LSE’, and we have length 2 permutations ‘SE’ and ‘ES’. How do we incorporate the letter L into these permutations? We just insert it into every possible location in both strings: beginning, middle, and the end. So for ‘SE’ the result is: ‘LSE’, ‘SLE’, ‘SEL’. And for the string ‘ES’ the results is: ‘LES’, ‘ELS’, ‘ESL’. We inserted the character L to every possible location in all the strings. This is it!. We will just use a recursive algorithm and we’re done. Recurse until the string is of length 1 by repeatedly removing the first character, this is the base case and the result is the string itself (the permutation of a string with length 1 is itself). Then apply the above algorithm, at each step insert the character you removed to every possible location in the recursion results and return. Here is the code:

def permutations(word):
    if len(word)<=1:
        return [word]
 
    #get all permutations of length N-1
    perms=permutations(word[1:])
    char=word[0]
    result=[]
    #iterate over all permutations of length N-1
    for perm in perms:
        #insert the character into every possible location
        for i in range(len(perm)+1):
            result.append(perm[:i] + char + perm[i:])
    return result

We remove the first character and recurse to get all permutations of length N-1, then we insert that first character into N-1 length strings and obtain all permutations of length N . The complexity is O(N!) because there are N! possible permutations of a string with length N, so it’s optimal. I wouldn’t recommend executing it for strings longer than 10-12 characters though, it’ll take a long time. Not because it’s inefficient, but inherently there are just too many permutations.

This is one of the most common interview questions, so very useful to know by heart.