This question can be solved efficiently with a very clever trick. There is an array of non-negative integers. A second array is formed by shuffling the elements of the first array and deleting a random element. Given these two arrays, find which element is missing in the second array. Here is an example input, the first array is shuffled and the number 5 is removed to construct the second array.
The naive way to solve it is for every element in the second array, check whether it appears in the first array. Note that there may be duplicate elements in the arrays so we should pay special attention to it. The complexity of this approach is O(N^2). A more efficient solution is to sort the first array, so while checking whether an element in the first array appears in the second, we can do binary search. But we should still be careful about duplicate elements. The complexity is O(NlogN). If we don’t want to deal with the special case of duplicate numbers, we can sort both arrays and iterate over them simultaneously. Once two iterators have different values we can stop. The value of the first iterator is the missing element. This solution is also O(NlogN). Here is the algorithm for this approach:
def findMissingNumber1(array1, array2): array1.sort() array2.sort() for num1, num2 in zip(array1, array2): if num1!=num2: return num1 return array1[-1]
Let’s see whether we can do better. In most interviews, we would be expected to come up with a linear time solution. We can use a hashtable and store the number of times each element appears in the second array. Then for each element in the first array we decrement its counter. Once hit an element with zero count that’s the missing element. Here is the algorithm:
def findMissingNumber2(array1, array2): d=collections.defaultdict(int) for num in array2: d[num]+=1 for num in array1: if d[num]==0: return num else: d[num]-=1
The time complexity is optimal O(N) but the space complexity is also O(N), because of the hashtable. Ideally we would like to have constant space complexity. One possible solution is computing the sum of all the numbers in array1 and array2, and subtracting array2′s sum from array1′s sum. The difference is the missing number in array2. However, this approach is somewhat problematic. What if the arrays are too long, or the numbers are very large. Then overflow will occur while summing up the numbers.
By performing a very clever trick, we can achieve linear time and constant space complexity without any problems. Here it is: initialize a variable to 0, then XOR every element in the first and second arrays with that variable. In the end, the value of the variable is the result, missing element in array2. Classy, isn’t it? Here is the code:
def findMissingNumber3(array1, array2): result=0 for num in array1+array2: result^=num return result
Let’s analyze why this approach works. What happens when we XOR two numbers? We should think bitwise, instead of decimal. XORing a 4-bit number with 1011 would flip the first, third, and fourth bits of the number. XORing the result again with 1011 would flip those bits back to their original value. So, if we XOR a number two times with some number nothing will change. We can also XOR with multiple numbers and the order would not matter. For example, say we XOR the number n1 with n2, then XOR the result with n3, then XOR their result with n2, and then with n3. The final result would be the original number n1. Because every XOR operation flips some bits and when we XOR with the same number again, we flip those bits back. So the order of XOR operations is not important. If we XOR a number with some number an odd number of times, there will be no effect.
Above we XOR all the numbers in array1 and array2. All numbers in array2 also appear in array1, but there is an extra number in array1. So the effect of each XOR from array2 is being reset by the corresponding same number in array1 (remember that the order of XOR is not important). But we can’t reset the XOR of the extra number in array1, because it doesn’t appear in array2. So the result is as if we XOR 0 with that extra number, which is the number itself. Since XOR of a number with 0 is the number. Therefore, in the end we get the missing number in array2. The space complexity of this solution is constant O(1) since we only use one extra variable. Time complexity is O(N) because we perform a single pass from the arrays.
This question demonstrates the power of bitwise operations, and how to use them effectively to achieve optimal solutions. It’s one of my favorite interview questions.

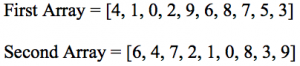
Gercekten guzeldi :)
Arden güzel soru – güzel cevap ancak tüm elemanları toplama fikri daha sade bence
kod yazarken senden sonra bakacak adamın anlayabilmesi de çok önemli bir proje için :)
Haklisin Ege okunabilirlik cok onemli tabi, ama interview’da asil amac en optimize sekilde cozmek. Hatta interviewer’in gormedigi orjinal guzel bir cozum uretirsen senden iyisi yok..
Peki ya xor yerine sum kullanirsak herhangi bir drawback’i olur mu sence?
Python’da sorun olmayacaktir. Cunku “Python seamlessly converts a number that becomes too large for an integer to a long. And long integers have unlimited precision”. Ama Python’da uzun listelerde XOR kisa listelerde sum daha hizli calisiyo.
Hey Arden,
Your solutions to the problem are brilliant! I like how you analyze various approaches and slowly lead the reader to the optimal solution (rather than presenting the reader with the best solution at the beginning).
Keep up the good work and thanks so much for sharing!
Hi Arden,
What about an alternative for the “adding up” solution as follows. Instead of summing the first and second array, then subtracting from each other, which can cause overflow, we can interleave between adding and subtracting. That is,
-take the 1st element in the 1st array
- subtract it from the 1st element in the 2nd,
- add to the 2nd element in the 1st array,
- subtract the result from the 2nd element in the 2nd array.
- so on.
We have an O(n) in time and O(1) in space. Let me know what you think. Thanks for your wonderful blog Ardan.
Thanks a lot for the comment. This is definitely a better solution than adding up, but it may also cause overflow. Imagine large numbers being in front of array1 and small numbers being in the end. And after shuffling array2 contains small numbers in front and large numbers move to the end. Then while subtracting and adding the sum will continually increase, which may lead to overflow. But this is the extreme worst case of course, and probably very unlikely to happen if we have a good shuffle function. Therefore, your approach is much better than simply adding up two arrays first and then subtracting. Because now the intermediate sum increases much slowly. Thanks for noticing. I hope you enjoy the blog..