Programming Interview Questions 7: Binary Search Tree Check

This is a very common interview question. Given a binary tree, check whether it’s a binary search tree or not. Simple as that..

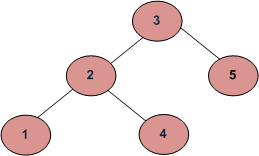
The first solution that comes to mind is, at every node check whether its value is larger than or equal to its left child and smaller than or equal to its right child (assuming equals can appear at either left or right). However, this approach is erroneous because it doesn’t check whether a node violates any condition with its grandparent or any of its ancestors. The following tree would be incorrectly classified as a binary search tree, the algorithm won’t be able to detect the inconsistency between 3 and 4:

So, we should keep track of the minimum and maximum values a node can take. And at each node we will check whether its value is between the min and max values it’s allowed to take. The root can take any value between negative infinity and positive infinity. At any node, its left child should be smaller than or equal than its own value, and similarly the right child should be larger than or equal to. So during recursion, we send the current value as the new max to our left child and send the min as it is without changing. And to the right child, we send the current value as the new min and send the max without changing. This approach leads to the following code:

class Node:
    def __init__(self, val=None):
        self.left, self.right, self.val = None, None, val
 
INFINITY = float("infinity")
NEG_INFINITY = float("-infinity")
 
def isBST(tree, minVal=NEG_INFINITY, maxVal=INFINITY):
    if tree is None:
        return True
 
    if not minVal <= tree.val <= maxVal:
        return False
 
    return isBST(tree.left, minVal, tree.val) and \
           isBST(tree.right, tree.val, maxVal)

There’s an equally good alternative solution. If a tree is a binary search tree, then traversing the tree inorder should lead to sorted order of the values in the tree. So, we can perform an inorder traversal and check whether the node values are sorted or not. Here is the code:

def isBST2(tree, nodes=[NEG_INFINITY]):
    if tree is None:
        return True
 
    if not isBST2(tree.left, nodes):
        return False   
 
    if tree.val < nodes[-1]:
        return False
 
    nodes.append(tree.val)
 
    return isBST2(tree.right, nodes)

I personally like this question a lot because it’s simple (but not trivial) and demonstrates the basic knowledge of binary search trees and tree traversals.